数学では、体積を求める問題が頻出します。体積を求める問題は、体積を求める公式を覚えていないと解くことができません。今回は、主要な図形の体積を求める公式についてまとめました。基本的には、中学校を卒業するまでに学習する公式をまとめたつもりですが、過不足があるかもしれません。
体積の公式
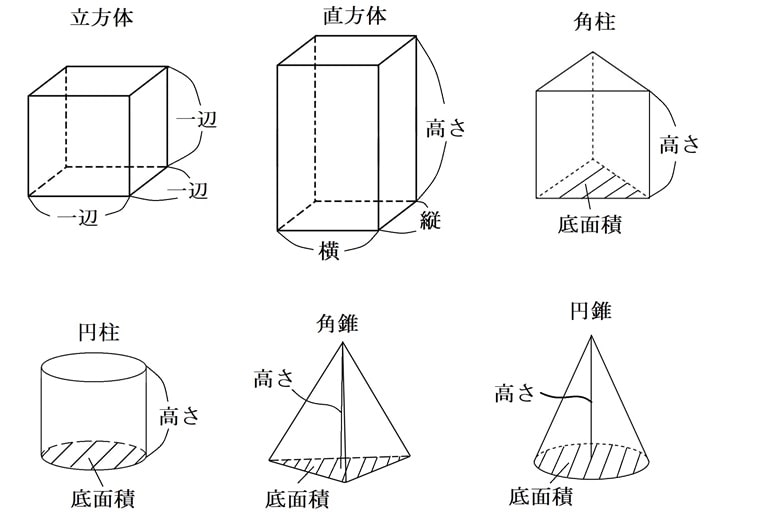
・立方体
一辺×一辺×一辺
・直方体
縦×横×高さ
・角柱
底面積×高さ
・円柱
底面積×高さ
・角錐
底面積×高さ÷3(×1/3)
・円錐
底面積×高さ÷3 (×1/3)
立方体は、角柱の一種といえます。一辺×一辺×一辺は、底面積×高さと同じです。直方体も角柱の一種といえます。縦×横は、底面積といえるため、縦×横×高さも、底面積×高さと同じです。角錐と円錐は、同じ式で体積を求めることできます。したがって、柱と錐の2つの体積の公式を覚えておけば、上記した立体の体積は求めることができます。
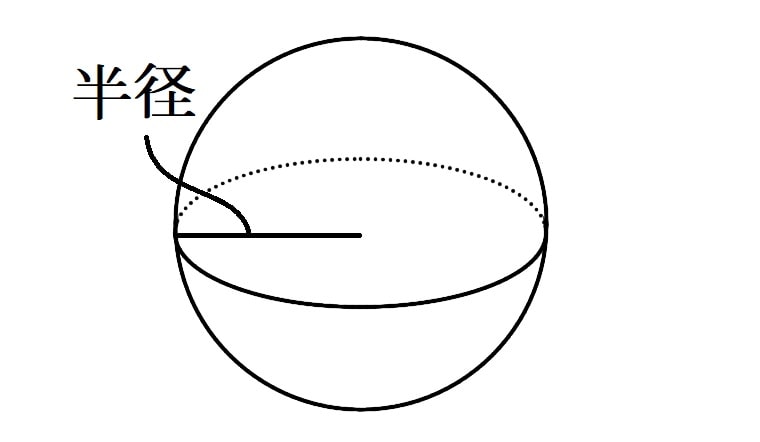
・球
4/3×円周率×半径3
円周率は、πとも表記されます。一般的には、3.14が用いられます。
確認テスト
[問題]
問1:一辺が3cmの立方体の体積はいくつか。
問2:体積が30cm3の直方体がある。この直方体の縦は3cm、横は5cmである。高さは何cmか。
問3:直径が8cm、高さが4cmの円柱がある。この円柱の体積を求めよ。ただし、円周率は3.14とする。
問4:底面が正方形の四角柱がある。底面の一辺の長さは4cm、四角柱の高さは5cmである。この四角柱の体積を求めよ。
問5:底面が正方形の四角錐がある。底面の一辺の長さは4cm、四角錐の高さは5cmである。この四角錐の体積を求めよ。
問6:底面の半径が4cm、高さが3cmの円錐の体積を求めよ。 ただし、円周率は3.14とする。
問7:体積が78.5cm3の円錐がある。この円錐の底面積が78.5cm2の場合、円錐の高さは何cmか。
問8:半径3cmの球の体積を求めよ。ただし、円周率は3.14とする。
[解答・解説]
問1:3×3×3=27cm3
問2:30÷3÷5=2cm
問3:4×4×3.14×4=200.96cm3
問4:4×4×5=80cm3
問5:4×4×5÷3=80/3cm3
問6:4×4×3.14×3÷3=50.24cm3
問7:底面積×高さ÷3=体積なので、高さ÷3=1になれば、底面積=体積になる。このため、高さは3cm
問8:4/3×3.14×3×3×3=113.04cm3
動画で体積の公式をおぼえよう!
ポテスクールの動画「体積の公式をおぼえよう!」は、体積の公式を覚えるための動画です。このページで紹介した体積の公式については、上の動画で学習することができます。動画も活用して、体積の求め方をマスターしてください!