
つるかめ算は、特殊算の1つです。特殊算とは、主として中学受験に必要とされる算数の解法で、つるかめ算以外にも多くのものがあります。このため、中学受験に縁のない方にとっては、特殊算は不要と考えることもできます。しかし、つるかめ算は、日常生活でも役に立ちます(あるいは、日常生活で既に無意識に使用しているかもしれません)。このため、つるかめ算の考え方を理解することは、決して損にはならないと思います。今回は、つるかめ算について解説していきます。
つるかめ算とは
つるかめ算とは、つるの足の数と、かめの足の数との違いに着目した解法です。
例えば、つるとかめの合計数と、つるの足とかめの足の合計数の両方がわかっているときに、これらの合計数からつるの数とかめの数を求めることができます。つるの足の数は2本で、かめの足の数は4本です。この差を利用してつるの数とかめの数を求めるのがつるかめ算です。
つるとかめの合計数が2匹で、つるの足とかめの足の合計数が6本であれば、つるは1匹、かめは1匹です。つるとかめの合計数が3匹で、つるの足とかめの足の数の合計数が8本であれば、つるは2匹、かめは1匹です。このように、つるとかめの合計数と、つるの足の数とかめの足の数の合計数が決まっていれば、つるとかめが何匹ずついるかわかります。
なお、つるかめ算の「つる」と「かめ」は一例であり、実際の問題では、つるとかめ以外について問われることもあります。つるかめ算とは、2つの物が存在している場合に、2つの物の合計数から、それぞれの物の数を算出する考え方ともいえます。
つるかめ算の解き方
・式を使った解き方
かめの数=(つるの足とかめの足の合計数-つるとかめの合計数×2)÷2
つるの数=(つるとかめの合計数×4-つるの足とかめの足の合計数)÷2
上記した2つの式でつるの数とかめの数を求めることができます。
つるの数がわかれば、つるとかめの合計数からつるの数を引くことで、かめの数がわかります。同様に、かめの数がわかれば、つるの数もわかるので、上の式でどちらかの数を求めればいいです。
・式を使わない解き方
上の式を暗記していなくても、つるかめ算の考え方を理解できていれば、つるかめ算の問題は解くことができます。つるかめ算の考え方は、全てがつる(あるいはかめ)とした場合の足の数と、実際の足の数(問題に書かれた足の合計数)の差から、全てがつるの状態から何匹をかめに入れ替えればいいかを求めることです。例題を挙げて説明します。
例題:つるとかめの合計数が4匹、足の合計数が12本の場合に、つるの数とかめの数を求めよ。
[4匹全てをつるとした場合の解法]
4匹全てをつるとした場合、足の合計数は8です。実際の足の数は12なので、12-8で、実際の足の数のほうが足が4本多いです。
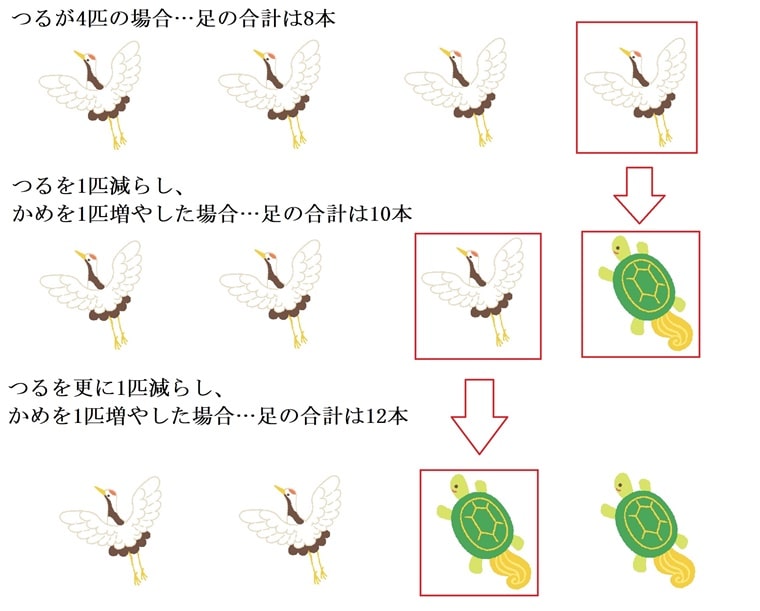
つるとかめの合計数は、決まっているので、上の図のように、つるを1匹減らせばかめが1匹増えます。つるが1匹減り、かめが1匹増えたときに、足の数が何本増えるかがつるかめ算の重要なポイントです。つるの足は2本、かめの足は4本なので、つるを1匹減らし、かめを1匹増やせば、足の合計数は2本増えることになります。
4匹全てをつるとした場合、実際の足の数に比べて、足が4本少なかったので、かめを増やして足の数を4本増やします。かめを1匹増やす毎に足の合計数は2本ずつ増えていくので、4÷2=2です。4匹全てがつるの状態から、かめを2匹増やし、その分つるを減らすので、つるは2匹、かめは2匹となります。
[4匹全てをかめとした場合の解法]
4匹全てをかめとした場合、足の合計数は16です。実際の足の数は12なので、16-12で、実際の足の数のほうが4本少ないです。
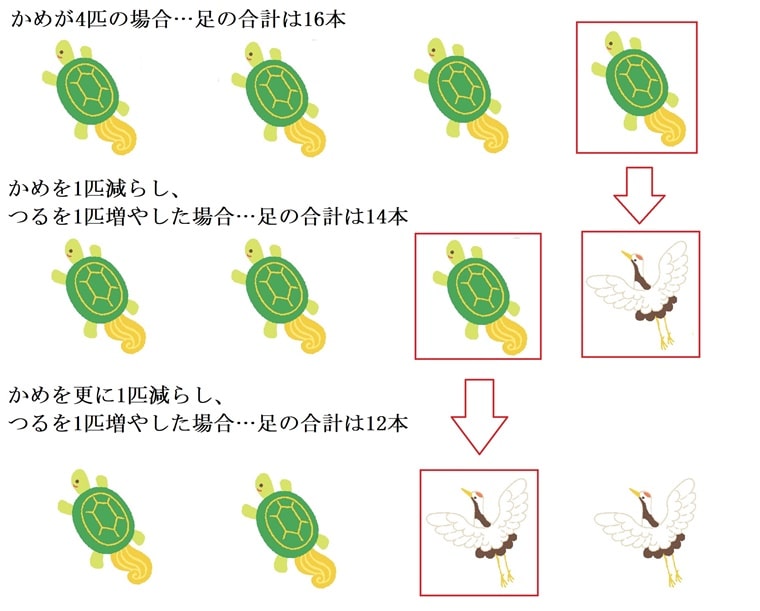
上の図のように、かめが1匹減り、つるが1匹増えたときに、足の合計数は2本減ることになります。4匹全てをかめとした場合、実際の足の数に比べて、足が4本多かったので、かめを減らして足の数を4本減らします。かめを1匹減らす毎に足の合計数は2本減っていくので、4÷2=2です。4匹全てがかめの状態から、かめを2匹減らし、その分つるを増やすので、つるは2匹、かめは2匹となります。
・式を再確認
つるかめ算の式は、上記したつるかめ算の考え方を反映したものになっています。つるかめ算の式をもう1回見てみましょう。
かめの数=(つるの足とかめの足の合計数-つるとかめの合計数×2)÷2
つるとかめの合計数×2をすることで(赤字部分)、全てがつるの場合の足の数を求めることができます。この数をつるの足とかめの足の合計数(青字部分)から引くことで、全てがつるとした場合の足の数と、実際の足の数の差を求めることができます。つるとかめの合計数に掛けられる”2″は、つるの足の数ということです。つるとかめであれば、”2″でいいですが、この数は問題に合わせて変化させる必要がある数といえます。
全てをつるとした場合の足の数と、実際の足の数の差を2で割ることで、何匹をかめに入れ替えればいいかを求めることができます。「÷2」の2は、つるの足の数とかめの足の数の差で、つるを1匹減らし、かめを1匹増やしたときに増える足の数です。
このように、上の式は、全てをつるとした場合の足の数と、実際の足の数の差から、全てがつるの状態から何匹をかめに入れ替えればいいかを式で表しただけにすぎません。上の式は、全てをつるとした場合でしたが、全てをかめとした場合の式であっても、同様のことがいえます。全てをかめとした場合の式”つるの数=(つるとかめの合計数×4-つるの足とかめの足の合計数)÷2 “であれば、 つるとかめの合計数×4の”4″を問題に合わせて変化させる必要があります。
面積図を使った解き方
つるかめ算の問題は、面積図で解くこともできます。先ほどと同じ例題を使って、面積図を使った場合の解き方を説明します。
例題:つるとかめの合計数が4匹、足の合計数が12本の場合に、つるの数とかめの数を求めよ。
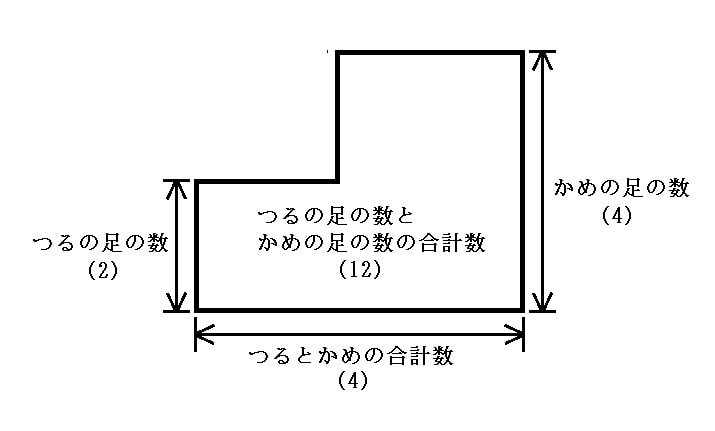
まず、上の図のように横をつるとかめの合計数、縦の1つをつるの足の数、縦のもう1つをかめの足とする図形を描きます。四角形が並んだような図形ができます。この図形の面積は、つるの足とかめの足の合計数(例題では12)を表しているとします。横の長さの比率が正確ではないため、実際にはつるの足とかめの足の合計数を表していない場合もありますが、問題を解く上ではつるの足とかめの足の合計数を表していると考えて差し支えありません。
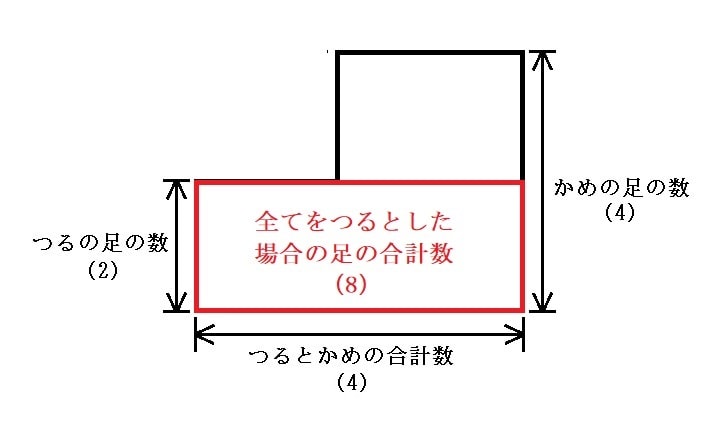
ここで、4匹全てをつるとした場合の足の合計数は、赤い部分の面積で表すことができます。例題では、赤い部分の面積は8です。
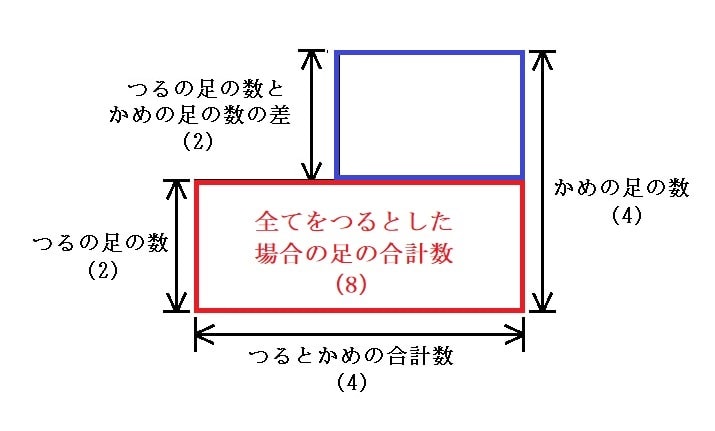
全体の面積が12で、赤い部分の面積が8なので、残りの青い部分の面積は4になります。面積を12にするには、赤い部分の面積に青い部分を足して12にしなければいけません。青い部分の面積は4で、青い部分の縦はかめの足の数-つるの足の数なので、2になります。したがって、4÷2で青い部分の横は2になります。青い部分の横は、かめの数を表しているので、つるは2匹、かめは2匹となります。
確認テスト
[問題]
問1:1つ100円のチョコレートと1つ150円のガムを合計20個買うと、合計金額は2600円でした。チョコレートの数とガムの数をそれぞれ求めなさい。
問題2:校庭は1周200mあります。この校庭を5周走ります。途中までは毎分150mで走り、途中からラストスパートをかけて毎分200mで走りました。校庭を5周走るのに6分かかりました。毎分150mで走った時間と毎分200mで走った時間をそれぞれ求めなさい。
[解答・解説]
問1:20個全てをチョコレートとすると、合計金額は100×20で2000円です。実際の合計金額との差は600円です。
チョコレート1個の金額とガム1個の金額との差は50円なので、600÷50=12で、ガムの数は12個になります。
答え…ガム12個、チョコレート8個
問2:200m×5周で合計1000m走ります。6分間を常に毎分150mで走ったとすると、走行距離は900mです。実際の走行距離との差は100mです。毎分150mで走ったときと毎分200mで走ったときの1分間の走行距離の差は50mです。このため、100÷50=2で、毎分200mで走った時間は2分になります。
答え…毎分150mで走った時間は4分、毎分200mで走った時間は2分。
動画でつるかめ算を学習しよう!
ポテスクールの動画「鶴亀算を学習しよう!」では、つるかめ算の解き方を解説しています。動画でつるかめ算を学びたいという方は、動画を参考にしてください。「面積図で鶴亀算を学習しよう!」では、面積図を使った解き方を学ぶことができます。こちらも活用してください。

