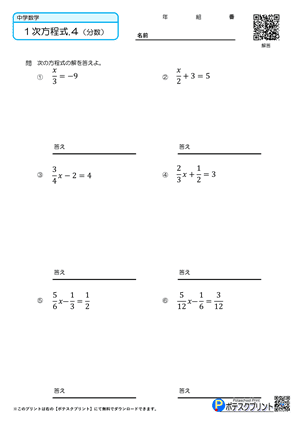
中学1年数学【1次方程式～計算問題～】練習プリント・演習問題・確認テスト用紙
中学１年数学【1次方程式～計算問題～】の練習プリント・演習問題・確認プリントです。定期テスト対策や受験対策にご使用ください。
【閑話休題】1次方程式とは？
【方程式とは？】
方程式とは、数学において、二つの式が等しいことを示すために使われる記号です。
具体的には、等号（=）を使って、二つの数学的な表現が等しいことを表します。
方程式は、未知数（通常は x や y などの文字）を含むことが多く、これらの未知数に対する値を求めることが目的となります。
以下に方程式の基本的な特徴を説明します。
1. 構成要素
- 左辺（LHS）: 等号の左側に書かれる数式。
- 右辺（RHS）: 等号の右側に書かれる数式。
例えば、2x+3=7 という方程式では、左辺は 2x+3 であり、右辺は 7 です。
2. 目的
方程式の主な目的は、未知数の値を見つけることです。上記の例では、未知数 xの値を求めることが求められます。
3. 種類
方程式にはさまざまな種類がありますが、いくつかの主要なものを以下に挙げます。
- 1次方程式: 未知数の最高次の指数が1である方程式（例：2x+3=7）。
- 2次方程式: 未知数の最高次の指数が2である方程式（例：x²−4x+4=0）。
- 連立方程式: 複数の方程式を同時に満たす未知数の値を求める方程式群。
4. 解法
方程式を解くとは、未知数の値を見つけることです。1次方程式の場合、単純な代数操作で解けますが、2次方程式やそれ以上の次の方程式の場合、特定の解法や公式が必要になることがあります。
【1次方程式の「1次」とは？】
1次方程式の「1次」という用語は、数学における「次（degree）」という概念から来ています。次とは、ある多項式の項の中で変数の指数（すなわち変数の上に付けられた数字）の最大値を指します。
具体的には、1次方程式とは、変数の最高次の指数が1である方程式のことです。例えば、方程式 ax+b=0では、変数 x の指数は1です。このため、この方程式は1次方程式と呼ばれます。
「1次」という用語の由来は、ラテン語の「gradus（階段）」に由来しており、これは「ステップ」や「段階」を意味します。この概念は、方程式の複雑さや変数の関係の度合いを示すために使用されます。
したがって、1次方程式は最も基本的な形の方程式であり、変数が1次の（つまり指数が1の）項しか持たないものを指します。